From LaPET electronics

Jump to: navigation, search

Contents

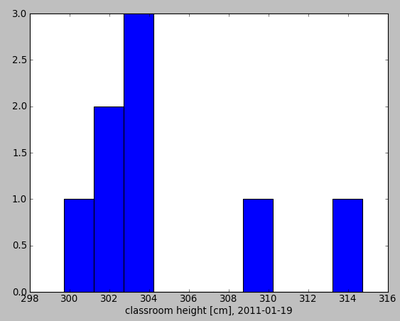
examples of distributions

classroom height, 2011-01-19
velocity distribution of gas molecules
U.S. household income distribution
Physics Today beam distributions
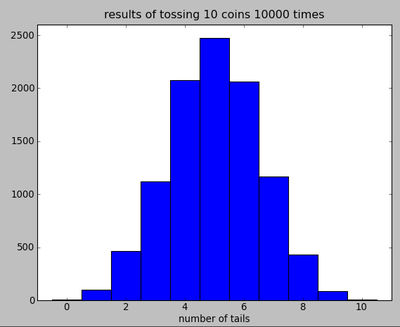
def toss():
    if random()<0.5: return 0
    return 1
def toss10():
    return sum([toss() for i in range(10)])
tosses = [toss10() for i in range(10000)]
clf(); hist(tosses,bins=11,range=(-0.5,10.5)); axis([-1,11,0,2600])
title("results of tossing 10 coins 10000 times")
xlabel("number of tails")
results of tossing 10 coins 10000 times

misc python definitions 

from scipy.misc import factorial
choose = lambda N,m: factorial(N)/factorial(m)/factorial(N-m)

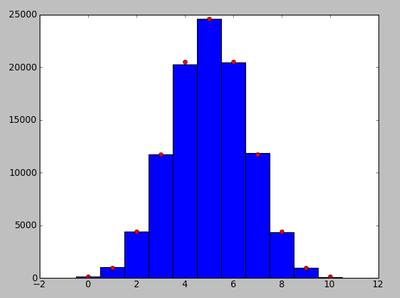
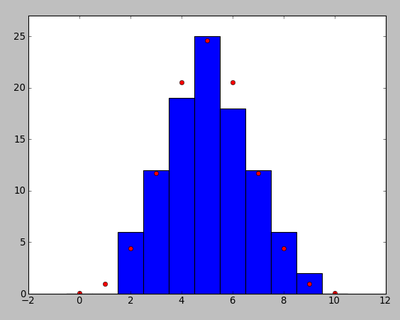
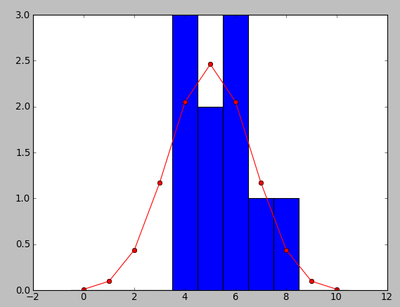
more on coin toss 

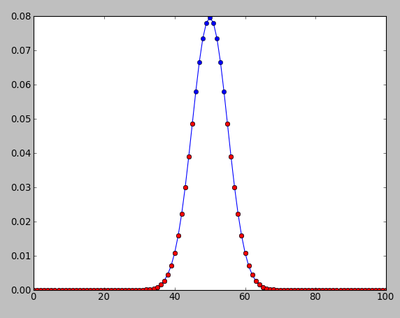
NNN=100000
clf(); hist([toss10() for i in range(NNN)],bins=11,range=(-0.5,10.5))
N=10; m=arange(N+1); P=choose(N,m)*0.5**N; plot(m,NNN*P,'ro');
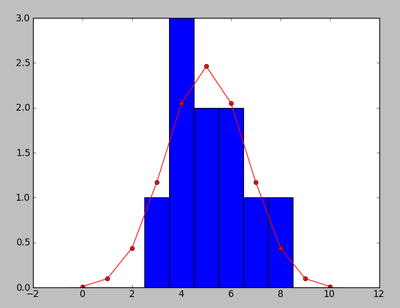
histogram of 100000 ten-coin tosses, with parent distribution (dots)
NNN=100
clf(); hist([toss10() for i in range(NNN)],bins=11,range=(-0.5,10.5))
N=10; m=arange(N+1); P=choose(N,m)*0.5**N; plot(m,NNN*P,'ro');
axis([-2,12,0,27])
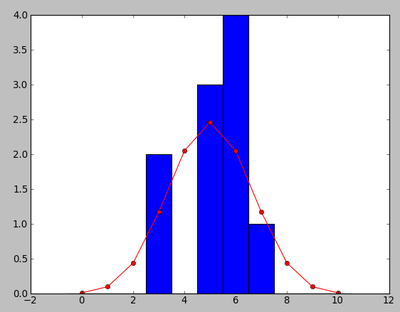
histogram of 100 ten-coin tosses, with parent distribution (dots)
NNN=10
clf(); hist([toss10() for i in range(NNN)],bins=11,range=(-0.5,10.5))
N=10; m=arange(N+1); P=choose(N,m)*0.5**N; plot(m,NNN*P,'ro-');
histogram of 10 ten-coin tosses, with parent distribution (connected dots)
histogram of 10 ten-coin tosses, with parent distribution (connected dots)
histogram of 10 ten-coin tosses, with parent distribution (connected dots)

summing area in tails of a distribution

  • Suppose you toss a (fair) coin 100 times. Mean number of tails is 50.
  • How often does a deviation of 5 or more (in either direction) occur?
    • Looks like about 37% of the time. 
N=100; m=arange(N+1); P=choose(N,m)*0.5**N
clf(); plot(m,P,'o-')
plot(m[:46],P[:46],'ro')
plot(m[55:],P[55:],'ro')
sum(P[:46])
sum(P[55:])
sum(P[:46])+sum(P[55:])

In [253]: sum(P[:46])
Out[253]: 0.18410080866334808

In [254]: sum(P[55:])
Out[254]: 0.1841008086633481

In [255]: sum(P[:46])+sum(P[55:])
Out[255]: 0.36820161732669621
how unlikely is it to see 45 tails in 100 coin tosses?
  • How often does a deviation of 40 or more occur?
    • Looks like about 3×10-17 
In [258]: sum(P[:11])
Out[258]: 1.5316450877189926e-17

In [259]: sum(P[90:])
Out[259]: 1.5316450877189926e-17

In [260]: sum(P[:11])+sum(P[90:])
Out[260]: 3.0632901754379851e-17

roll dice

  • roll 10 dice 
N=10; p=1.0/6; m=arange(N+1); P=choose(N,m)*p**m*(1-p)**(N-m)
clf(); plot(m,P,'o-'); axis([-1,11,-0.005,.36])
how many ones in 10 dice


  • roll 100 dice 
N=100; p=1.0/6; m=arange(N+1); P=choose(N,m)*p**m*(1-p)**(N-m)
clf(); plot(m,P,'o-'); axis([-1,40,-0.001,.13])
how many ones in 100 dice


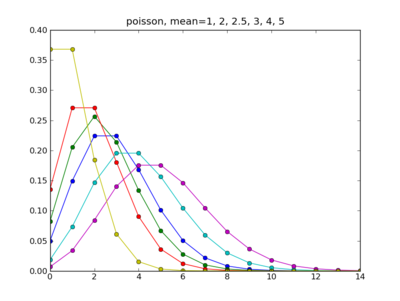
poisson distribution 

clf()
mu=1.0; m = arange(15); P = mu**m*exp(-mu)/factorial(m)
plot(m,P,'o-')
mu=2.0; m = arange(15); P = mu**m*exp(-mu)/factorial(m)
plot(m,P,'o-')
mu=2.5; m = arange(15); P = mu**m*exp(-mu)/factorial(m)
plot(m,P,'o-')
mu=3.0; m = arange(15); P = mu**m*exp(-mu)/factorial(m)
plot(m,P,'o-')
mu=4.0; m = arange(15); P = mu**m*exp(-mu)/factorial(m)
plot(m,P,'o-')
mu=5.0; m = arange(15); P = mu**m*exp(-mu)/factorial(m)
plot(m,P,'o-')
title("poisson, mean=1, 2, 2.5, 3, 4, 5")

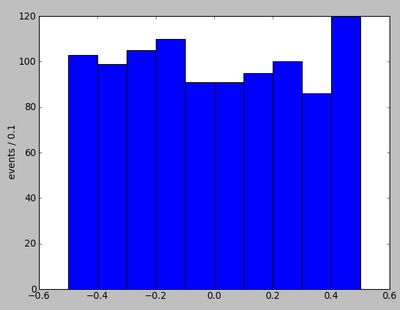
Note Poisson fluctuations in bin contents, e.g. for this (nominally flat) distribution from the homework example:

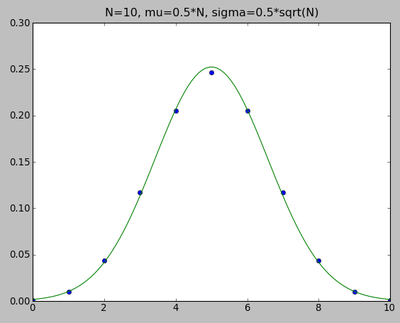
binomial vs. gaussian 

N = 10; m = arange(N+1); P = 0.5**N*choose(N,m)
mu=0.5*N; sig=0.5*sqrt(N); x=linspace(0,N,100); G = exp(-0.5*(x-mu)**2/sig**2)/sig/sqrt(2*pi)
clf(); plot(m,P,'o'); plot(x,G,'-')
title(r"N=10, mu=0.5*N, sigma=0.5*sqrt(N)")
binomial vs. gaussian: N=10, p=0.5
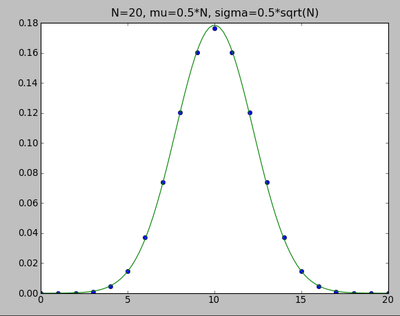
N = 20; m = arange(N+1); P = 0.5**N*choose(N,m)
mu=0.5*N; sig=0.5*sqrt(N); x=linspace(0,N,100); G = exp(-0.5*(x-mu)**2/sig**2)/sig/sqrt(2*pi)
clf(); plot(m,P,'o'); plot(x,G,'-'); title(r"N=20, mu=0.5*N, sigma=0.5*sqrt(N)")
binomial vs. gaussian: N=20, p=0.5
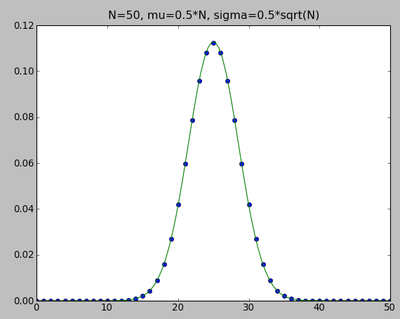
N = 50; m = arange(N+1); P = 0.5**N*choose(N,m)
mu=0.5*N; sig=0.5*sqrt(N); x=linspace(0,N,100); G = exp(-0.5*(x-mu)**2/sig**2)/sig/sqrt(2*pi)
clf(); plot(m,P,'o'); plot(x,G,'-')
title(r"N=50, mu=0.5*N, sigma=0.5*sqrt(N)")
binomial vs. gaussian: N=50, p=0.5

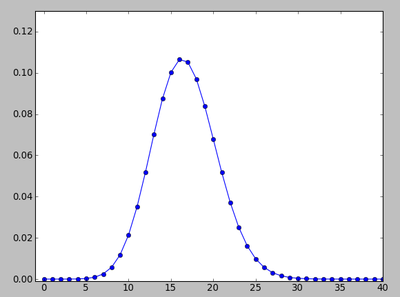
poisson vs. gaussian 

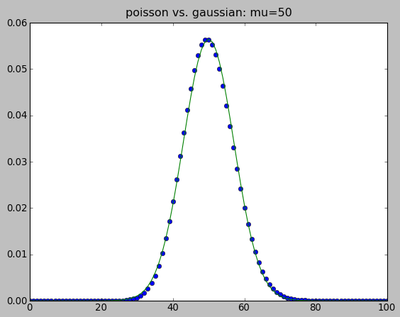
mu=50; m=arange(2*mu+1.0); poisson=mu**m*exp(-mu)/factorial(m); gauss=exp(-0.5*(m-mu)**2/mu)/sqrt(2*pi*mu)
clf(); plot(m,poisson,'o'); plot(m,gauss,'-')
title("poisson vs. gaussian: mu=50")
poisson vs. gaussian: mu=50
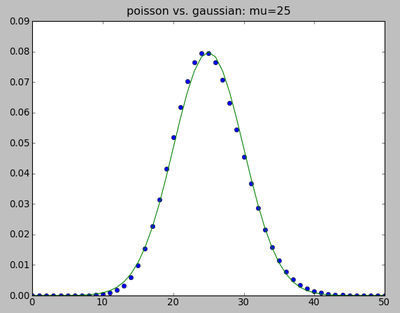
mu=25; m=arange(2*mu+1.0); poisson=mu**m*exp(-mu)/factorial(m); gauss=exp(-0.5*(m-mu)**2/mu)/sqrt(2*pi*mu)
clf(); plot(m,poisson,'o'); plot(m,gauss,'-')
title("poisson vs. gaussian: mu=25")
axis([0,50,0,0.09])
poisson vs. gaussian: mu=25
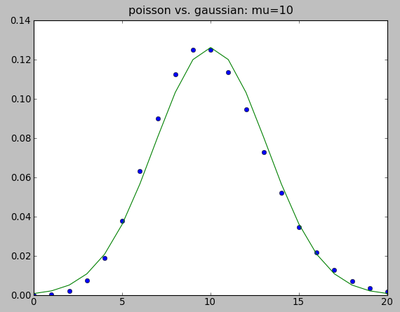
mu=10; m=arange(2*mu+1.0); poisson=mu**m*exp(-mu)/factorial(m); gauss=exp(-0.5*(m-mu)**2/mu)/sqrt(2*pi*mu)
clf(); plot(m,poisson,'o'); plot(m,gauss,'-')
title("poisson vs. gaussian: mu=10")
poisson vs. gaussian: mu=10
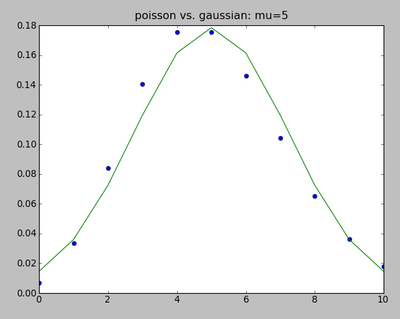
mu=5; m=arange(2*mu+1.0); poisson=mu**m*exp(-mu)/factorial(m); gauss=exp(-0.5*(m-mu)**2/mu)/sqrt(2*pi*mu)
clf(); plot(m,poisson,'o'); plot(m,gauss,'-')
title("poisson vs. gaussian: mu=5")
poisson vs. gaussian: mu=5
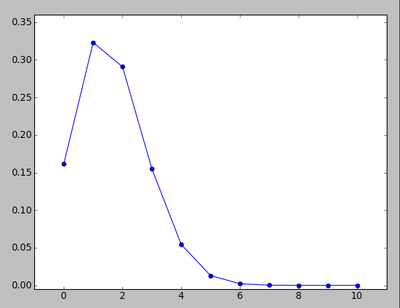
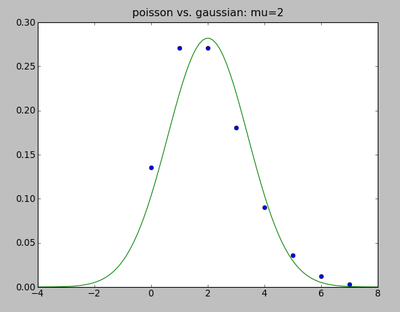
mu=2; m=arange(8); poisson=mu**m*exp(-mu)/factorial(m)
mm=linspace(-4,8,100); gauss=exp(-0.5*(mm-mu)**2/mu)/sqrt(2*pi*mu)
clf(); plot(m,poisson,'o'); plot(mm,gauss,'-')
title("poisson vs. gaussian: mu=2")
poisson vs. gaussian: mu=2